Outreach

This page collects parts of research made available in the past to a broader community, and other interesting things which make X-ray astronomy cool!

My interview to RTF1 about eRosita bubbles

Following the discovery paper which I'm happy to be part of, I were approached by local Neckar-Alb TV channel RTF1, who wanted to learn about how Tuebingen is involved. This resulted in an interview in a bad German (from my side), and good German (from Chris Tenzer) which you can also find on youtube:

I've also prepared for them a longer and higher-res animation of the bubbles moving over Tuebingnen which was featured on RTF1, and an artistic view of them over Tuebingen (click for high resolution) Feel free to use as wallpaper etc, or share giving appropriate credit!

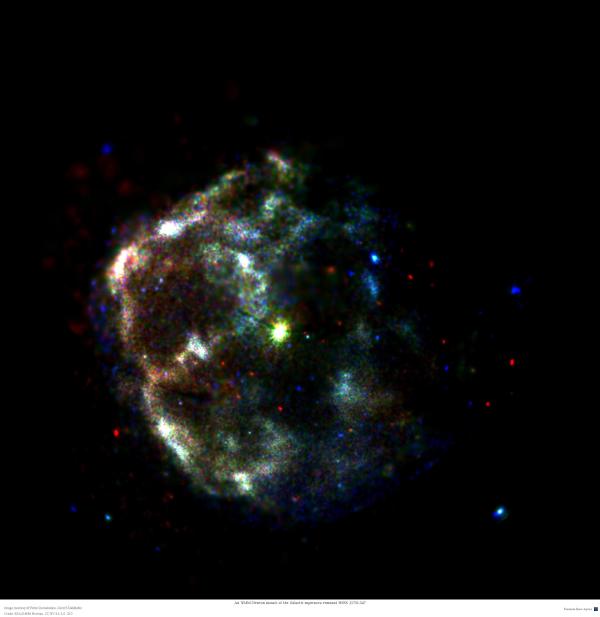
XMM-Newton image of SNR HESS J1731-347

I've spent quite a bit of time working on this rather unique supernova remnant (first discovered in TeV!). Among other things, it resulted in a rather long paper where one of the most complex analyses of XMM data ever published is presented. The spectral fit described there involved simultaneous fitting of ~200 spectra from five individual XMM observations, each with separate backgrounds, responses, and variable stray-light from a nearby LMXB. This analysis allowed to illustrate that SNR is indeed interacting with nearby molecular cloud and so part of the observed TeV emission could in fact be hadronic. This means that this SNR can be considered as a cosmic ray accelerator, which is not unexpected but nice! As a side effect of this research we obtained an image of the SNR which you can see below, and which was also featured in XMM-Newton image gallery

Luminosity function of Galactic X-ray binaries and implications for eRosita

Back in 2014 we were preparing for the launch of eRosita and tried to make forecasts for what it would see in context of our favorite objects, i.e. X-ray binaries. This requited re-assing data from INTEGRAL and Swift observatories and modeling of the spatial distribution of XRBs in the Milky way, which was presented in a short paper. This research was considered by INTEGRAL as a nice illustration of power of coded-mask imaging and was featured as picture of the month. The animation is also shown below. The main idea behind the paper is that the X-ray luminosities of accreting compact object binaries are known to follow a broken power-law distribution, spanning for at least six orders of magnitude in luminosity. Most of the sources are thus expected to be faint and, therefore, hard to observe. This makes it hard to constrain the parameters of the luminosity distribution (or X-ray luminosity function, XLF), which is of key importance for understanding the origin and evolution of X-ray binaries (XRBs).

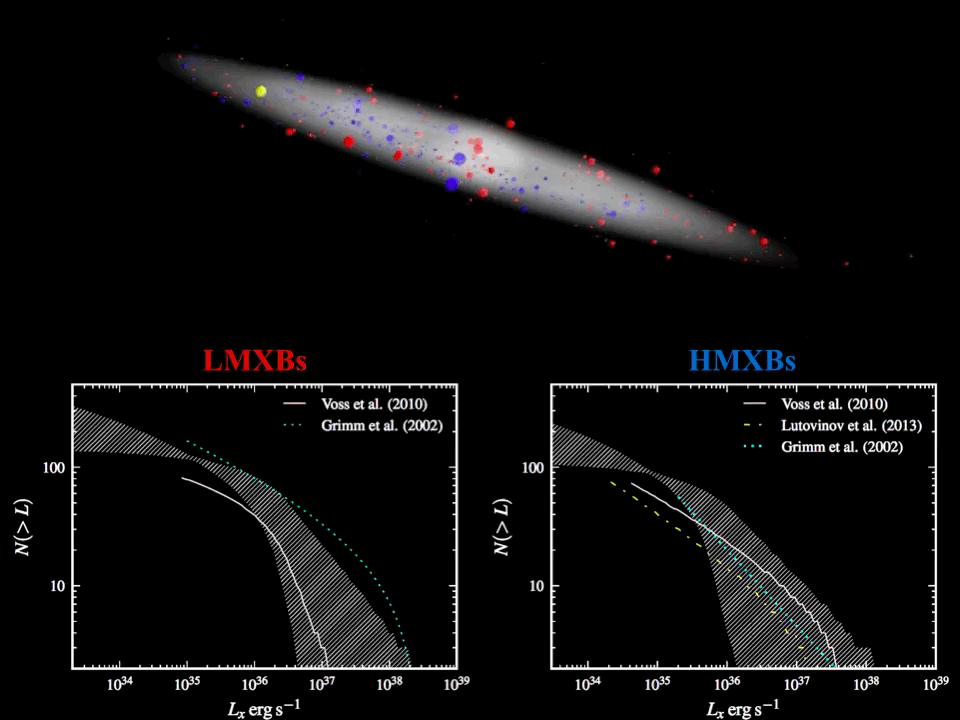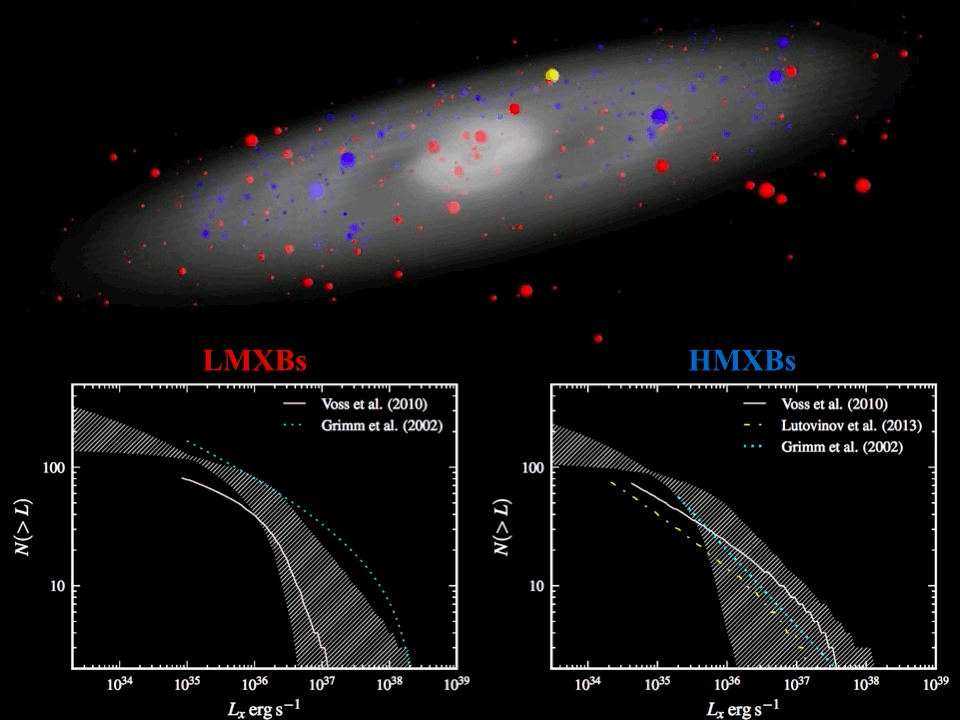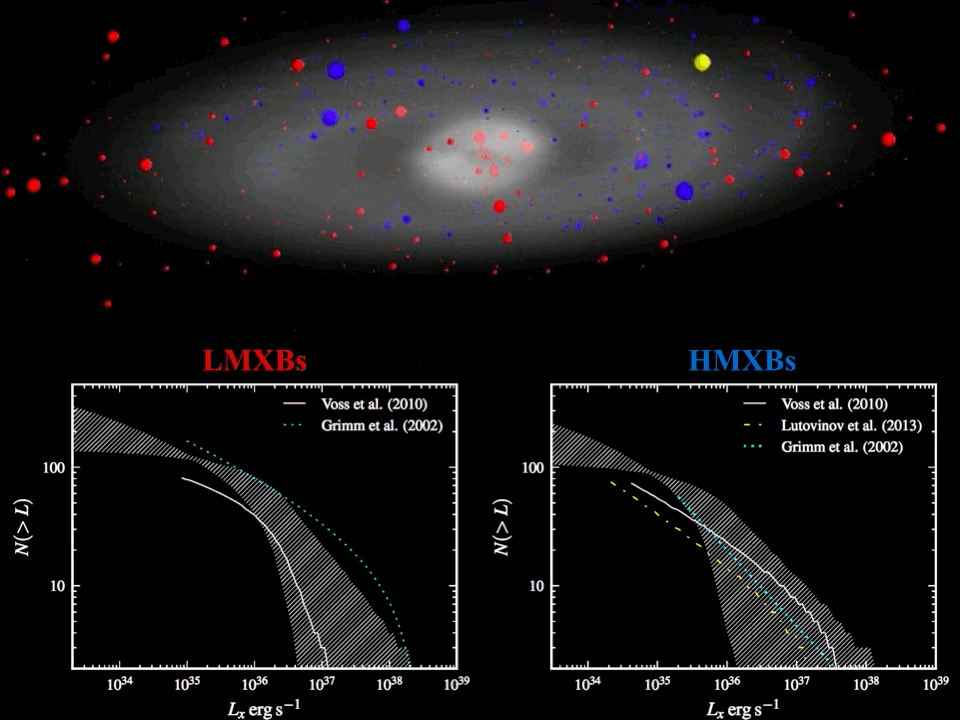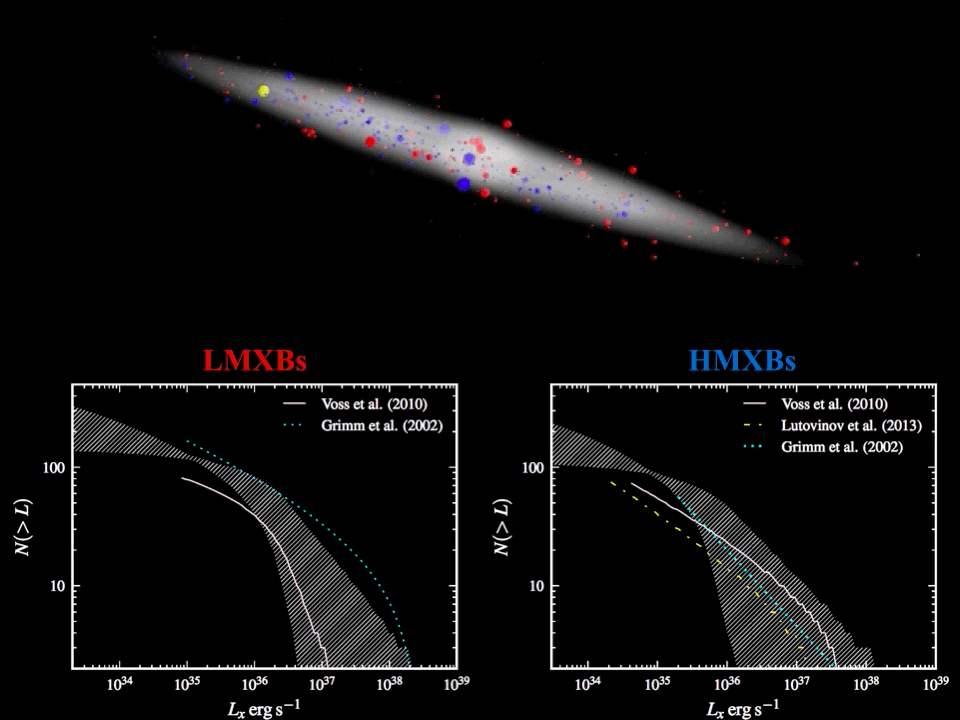
The XLF is usually derived from the observed flux distribution of X-ray binaries with known distances. Since only a fraction of the entire population is normally observed, the derived XLF must then be corrected for incompleteness effects. Measuring distances is not trivial, so the sample of XRBs with known distances is rather small, which consequently implies large statistical uncertainties for the derived XLF parameters.

To overcome this problem, it is proposed to model the observed flux distribution of XRBs, rather than their luminosity distribution. This allows to substantially increase the size of the object sample. The fluxes of high-mass and low-mass X-ray binaries (HMXBs, LMXBs, respectively) derived from INTEGRAL/ISGRI 9-year survey are used as an observational reference, which is the most sensitive hard X-ray survey to date. To model the observed flux distribution, Monte-Carlo calculations are used to simulate the expected flux distribution from a synthetic XRB population. The animation in the top panel shows an example of the spatial distribution for simulated HMXB (blue) and LMXB (red) populations and their X-ray luminosity coded with the size of the symbol. For each artificial source, the flux which would be observed by INTEGRAL at Sun location (yellow point), can be easily calculated and the resulting flux distribution can be compared with observations. The parameters of the simulated XRB populations can then be adjusted so that the simulated flux distribution is consistent with observations.